Opis problema

Opis realnih situacija koje se sreću u praksi

Pretpostavimo da u neko naseljeno mjesto treba dovesti električnu energiju.Znamo da električne vodove moramo dovesti do svake kuće,pa nam te kuće kao i veća čvorišta – električni stubovi , predstavljaju čvorove nekog zamišljenog grafa.Ako želimo da utrošimo najmanju moguću količinu materijala – električnog kabla , tada nam je potreban nekakav matematički metod čijom upotrebom ćemo postići povezivanje svih čvorova ovog grafa a da pri tome ispunimo dva uvjeta : prvi , da količina utrošenog materijala bude najmanja moguća , prevedeno na jezik matematike da ukupna dužina svih grana grafa bude najmanje moguća i drugi , da povezivanjem čvorova ne napravimo zatvoreni ciklus.Drugi uvjet nam je potreban jer očito na jednu kuću ne trebaju dolaziti dva izvora napajanja dovoljan je samo jedan. Analogijom uviđamo da je broj ovakvih i njima sličnih problema koje susrećemo u praksi jako veliki , naime osim električne mreže sa ovim problemom se sučeljava i vodovodna , putna , željeznička i svaka druga vrsta komunikacije u mreži.

Odgovor na ove i njima slične probleme daje matematički metod kojeg nazivamo metodom najkraćeg stabla. Uvijek kada imamo problem povezivanja čvorova grafa (neovisno od toga šta ti čvorovi predstavljaju u realnom životu) uz uvjet zabrane zatvaranja ciklusa i glavni uvjet da je dužina stabla najmanja moguća (što predstavlja materijal koji se troši za uspostavljanje veze) koristimo ovaj metod.

Matematički model

Izvođenje matematičkog modela na osnovu opisnog,kratak komentar dobijenih relacija

Ako problem možemo izmodelirati (tj. izvući njegove primarne osobine i njih posmatrati) i ako je taj model ekvivalentan grafu onda je očito da na njegovo riješavanje možemo primjeniti znanja koje nudi teorija grafova.U tom kontekstu definisati ćemo graf kao skup njegovih elemenata i to:

· tačke/čvorovi – skup tačaka ai gdje je i iz N , 1≤ i ≤ n , n je broj čvorova grafa,

· grane – ivice koje spajaju čvorove grafa.

Ako na ovom skupu definišemo relaciju ρ kao udaljenost između dvaju čvorova grafa onda vrijedi:

a ρ b = b ρ a = dab ; gdje je dab pozitivan broj - dužina grane koja povezuje čvorove,

a ρ b = b ρ a = ∞ ; ako čvorovi a i b nisu spojeni granom.

Stablo je graf koji ne sadrži nijedan prost elementaran ciklus tj. ne sadrži nijednu konturu.

Primjer jednog grafa prikazan je na donjoj slici:

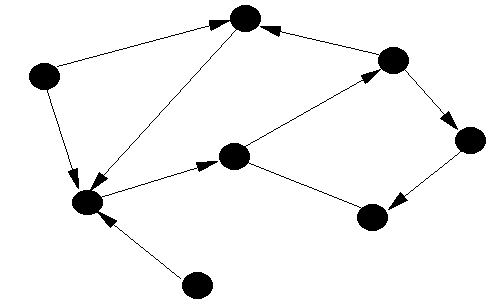
Uzmimo u obzir slijedeći problem.Na donjoj slici vidimo graf sa 5 čvorova i moguće kombinacije veza između tih čvorova tj.prikazane su moguće grane grafa.Ako želimo da u tom grafu pronađemo stablo najmanje dužine koje uključuje sve čvorove grafa a da pri tome ne bude zatvorena ni jedna kontura u grafu onda mi riješavamo problem pronalaženja najkraćeg stabla grafa.

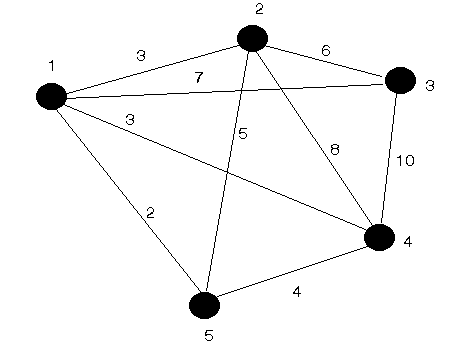Ovdje je,

ρ	1	2	3	4	5
1	∞	3	7	3	2
2	3	∞	6	8	5
3	7	6	∞	10	∞
4	3	8	10	∞	4
5	2	5	∞	4	∞

Npr. jedna moguća struktura za koju treba ispitati zadovoljava li gore definisane uslove je 1-2, 2-3, 3-4, 4-5. Možemo primjetiti:

· za graf od n čvorova riješenje uključuje n-1 grana grafa,

· riješenje se lako može dobiti primjenjujući određeni algoritam koji uključuje iteraciju (takvi su Primov i Kruskalov algoritam) i

· konačna struktura naziva se najkraćim stablom grafa.

Moguće metode riješenja

Primov i Kruskalov algoritam

Postoji više metoda za pronalaženje najkraćeg stabla grafa , naš program uključuje dvije veoma poznate a to su Primov i Kruskalov algoritam.

Primov algoritam

Primov algoritam je vrlo jednostavan za praćenje.Početna tačka se bira proizvoljno i ona odmah postaje dio grafa.Svaka sljedeća tačka se dodaje ako se ustanovi da je udaljenost između bilo koje tačke iz grafa i bilo koje slobodne tačke najmanja upravo za tu tačku i neku tačku koja je već u grafu.Postupak se iterativno nastavlja sve dok sve ne ostane ni jedna slobodna tačka , odnosno dok sve tačke ne budu uključene u graf. Jezikom pseudocoda :

1. Izaberi proizvoljan početni čvor,

2. Nađi njemu najbliži čvor i taj čvor postaje dio grafa,

3. Nađi grafu najbliži slobodni čvor,

4. Iterativno ponavljaj postupak pod tačkom 3. dok svi čvorovi ne budu uključeni u graf.

Kruskalov algoritam

Kruskalov algoritam za pronalaženje najkraćeg stabla grafa je tkzv. sebični (greedy) algoritam zbog toga što on obrađuje uvijek najmanju dostupnu ivicu (granu) grafa.Grane kandidati za ulazak u graf jesu sve moguće kombinacije početnih tačaka s tim što se izbjegava dupliranje grana npr. grana a→ b je jednaka grani b→a pa granu b→a ne treba uključivati u moguće kombinacije.Grafu se priključuje najmanja dostupna grana pazeći da se pri tome ne zatvori ciklus.Jezikom pseudocoda,

1. Sortirati sve grane-kandidate za ulazak u graf,

2. Priključi najmanju granu grafu ako se tim priključivanjem ne zatvara ciklus,

3. Iterativno ponavljaj postupak pod tačkom 2. dok sve početne tačke ne postanu dio grafa.

Detaljni opisi korištenih metoda

Primov i Kruskalov algoritam

U ovom dijelu ćemo detaljno pokazati ,kroz narativnu i grafičku prezentaciju, logički model algoritama.

Primov algoritam

Primov algoritam radi sa čvorovima kao objektima,jedan čvor je deklarisan kao slog CvorTip = record

imecvora : string;

xkoor : integer;

ykoor : integer;

end;

U našem riješenju primarni ključ za jedinstvenu identifikaciju jednog čvora jeste njegov položaj na radnom dijelu forme programa tj. uređeni par (xkoor,ykoor).

Čvor se ne može povezivati sam sa sobom.

Postoje dvije liste čvorova,lista slobodnih čvorova Ls i lista čvorova najkraćeg stabla Lg.Obje liste sadrže slogove sa istim opisom kao slog CvorTip s tim što postoji još polje slijedeci:pok_na_CvorTip koje predstavlja pokazivačku varijablu na slijedeći čvor u listi.

Rad algoritma:

Upotrijebićemo narativnu i grafičku prezentaciju procesa koji se odvijaju nad slobodnim čvorovima grafa (čvorovi sadržani u listi Ls) i kako oni postaju čvorovi grafa Lg.

Jezikom pseudocoda:

1. za čvor grafa koji korisnik unosi na radnu površinu formiraj slog tipa CvorTip ,

2. dodaj slog na kraj liste Ls-liste slobodnih čvorova,

3. ponavljaj korake 1. i 2. dok korisnik ne pritisne dugme Nadji najkraće stablo…,

4. prebaci prvi element liste Ls u listu Lg – listu čvorova pridruženih najkraćem stablu,

5. izmjeri udaljenost svakog pojedinačnog elementa iz Lg sa svakim pojedinačnim elementom iz liste Ls,

6. iz para čvorova (čvor1,čvor2) gdje je čvor1 iz Lg ,a čvor2 iz Ls,i za koje vrijedi da je udaljenost d12 minimalna,prebaci čvor2 iz Ls u Lg,

7. povuci liniju na ekranu između čvora1 i čvora2 (moveto(x1,y1);lineto(x2,y2)),

8. ponavljaj korake 5., 6., 7., dok lista Ls ne bude prazna.

Grafička prezentacija procesa:

Na Slici 1 vide se ulazi i izlazi iz Primovog Algoritma.Na njegovom ulazu je lista slobodnih cvorova Ls koja može biti napunjena ili od strane korisnika (novi projekat) ili iz prethodno spašenog projekta u datoteci sa ekstenzijom .mns. Na izlazu iz Primovog algoritma imamo napunjenu listu čvorova grafa Lg.U toku kreiranja ove liste na ekranu se crta sami graf a proces je gotov kada lista Ls bude prazna.Korisnik tekući projekat

može spasiti u odgovarajuću datoteku. Sliku 1 nazivamo kontekstnim nivoom opisa Primovog algoritma.

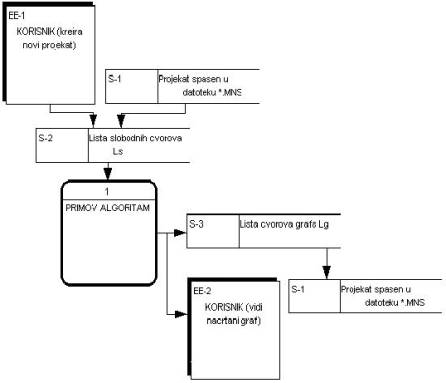
Slika 1. Ulazi i Izlazi iz Primovog Algoritma – Kontekst nivo procesa Primovog algoritma

Sa kontekst nivoa prelazimo na prvi nivo logičkog opisa procesa koji se odvijaju u Primovom algoritmu.

Na Slici 2 vidimo unutrašnjost Primovog algoritma.Na početku se bira proizvoljan čvor da bude prvi čvor od kojeg će proces krenuti.U našoj realizaciji to je prvi čvor u listi čvorova Ls.Zatim prelazimo na drugi proces a to je iterativno poređenje svih čvorova iz liste Ls sa svim čvorovima iz liste Lg.Slobodni čvor koji je najbliži grafu prebacuje se u listu Lg.Proces se ponavlja dok lista Ls ne bude prazna tj. dok svi čvorovi ne budu uključeni u graf.

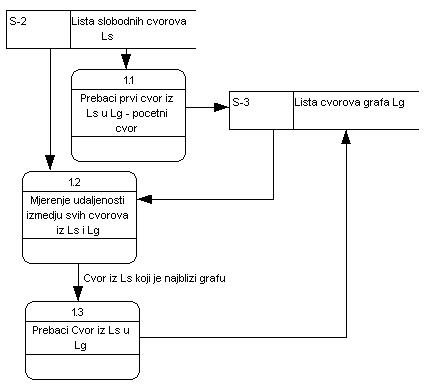
Slika 2. Prvi nivo razvoja Primovog Algoritma

Kao rezultat korisnik vidi nacrtani graf , i ima mogućnost spašavanja projekta u datoteku.

Kruskalov algoritam

Kruskalov algoritam radi sa granama kao objektima.Jedna grana grafa je opisana slogom:

Grana = record

imecvora1:string;

xkoor1:integer;

ykoor1:integer;

imecvora2:string;

xkoor2:integer;

ykoor2:integer;

duzina:real;

fragment:integer;

slijedeci:pokgrana;

end; Ključno polje koje primarno koristimo je polje fragment koje nam govori kom fragmentu pripada određena grana u nekom momentu.Primarni ključ koji se koristi za identifikaciju pojedine grane su polja imecvora1 i imecvora2 te iz tog razloga cvorovi ne mogu imati ista imena.Također je izbjegnuto i dupliranje grana.Kada korisnik unese cvorove grafa algoritam prvo kreira listu svih mogućih grana grafa (uz izbjegavanje dupliranja grana).Ova lista je sortirana.Opišimo algoritam,

Jezikom pseudocoda:

1 za čvor grafa koji korisnik unosi na radnu površinu formiraj slog tipa CvorTip ,

2 dodaj slog na kraj liste Ls-liste slobodnih čvorova,

3 ponavljaj korake 1. i 2. dok korisnik ne pritisne dugme Nadji najkraće stablo…,

4 formiraj listu Lk svih mogucih grana grafa,

5 sortiraj listu Lk,

6 uzmi element iz Lk i ispitaj da li oba cvora pripadaju istom fragmentu,ako da onda ne uključuj granu u najkraće stablo (jer se zatvara ciklus),inače priključi granu najkraćem stablu,

7 povuci liniju na ekranu između čvora1 i čvora2 (moveto(x1,y1);lineto(x2,y2)),

8 ponavljaj korak 6. i 7. za sve članove liste Lk.

Grafička prezentacija procesa:

Analogno slučaju kod Primovog algoritma,ulazi u Kruskalov algoritam su istovjetni.To mogu biti korisnik – koji "ručno" unosi čvorove grafa klikajući mišem po radnoj površini, i datoteka sa ekstenzijom *.mns u kojoj su već pohranjeni čvorovi ranije spašenog projekta.Na izlazu iz Kruskalovog algoritma je lista Lk u kojoj su sve grane grafa a iz koje su pojedine grane ekstraktovane i priključene najkraćem stablu po ranije opisanim standardima.Kontekst nivo procesa Kruskalovog algoritma izgleda kao na slici 1.,

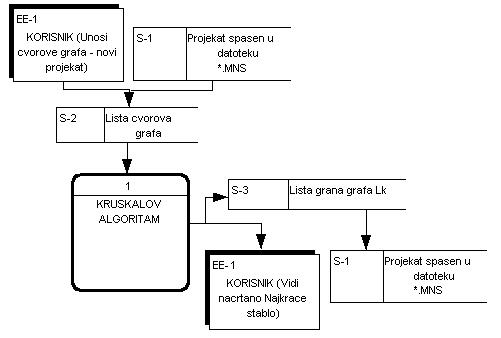
Slika 1. Ulazi i Izlazi iz Kruskalovog algoritma

Koji se procesi konkretno odvijaju u Kruskalovom algoritmu? Odgovor na ovo pitanje daje Slika 2.

Prvi proces jeste kreiranje svih mogućih grana grafa.Da ne bi došlo do dupliranja grana u kreiranju (npr.ako imamo čvorove 1. i 2. dovoljna nam je grana 1à2 a grana 2à1 neće biti kreirana) ,za to se brine podvučena linija koda.

pokcvor:=kglava;

repeat

temp1:=pokcvor.slijedeci;

repeat

…

temp1:=temp1.slijedeci;

until temp1=NIL;

pokcvor:=pokcvor.slijedeci;

until pokcvor.slijedeci=NIL;

Da je umjesto nje temp1:=kglava; imali bi dupliranje.Sledeći proces jeste umetanje grane na pravo mjesto tako da lista Lk bude sortirana po polju duzina.Kada dođemo do kraja liste čvorova završili smo sa kreiranjem liste grana.Dakle dobili smo sortiranu listu svih potencijalnih grana grafa.Grane se zatim priključuju najkraćem stablu.U ovom procesu ključnu ulogu ima polje fragment sloga grana.Generički ovo polje ima vrijednost 0. Ako oba čvora grane nisu zastupljena ni u jednoj grani dotad obrađenih grana tada se grani dodjeljuje nova vrijednost polja fragment.Kada dva čvora imaju različite vrijednosti polja fragment u dotad obrađenim granama grafa ta grana se pripaja najkraćem stablu s tim što se vrijednost ovog polja promijeni u svim granama koje imaju manju vrijednost ovog polja.Faktički dolazi do spajanja dva različita fragmenta po dodatoj grani.Ako dva čvora imaju istu vrijednost fragmenta u dotad obrađenim granama ta grana se preskače jer bi zatvorila ciklus.Postupak se nastavlja dok ne dođemo do kraja liste Lk.Slikom 2,

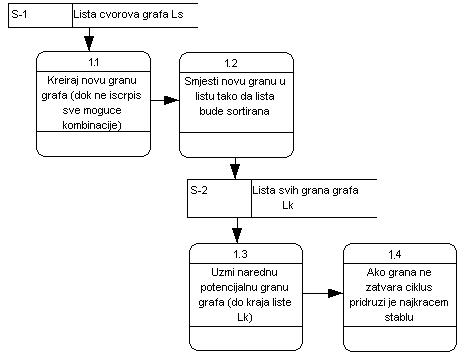
Slika 2.Prvi nivo razvoja Kruskalovog algoritma

Brojni primjer

Neka je korisnik zadao čvorove grafa kao na slici1.,sa datim čvorovima:

Slika1.Na radnoj površini programa korisnik klikom miša unosi čvorove grafa

Udaljenost između dva čvora izračunava se korištenjem jednačine za udaljenost tačaka u ravni pošto je svaki čvor definisan svojim imenom i (x,y) pozicijom na ekranu,u našem riješenju dmin = sqrt (sqr(xkoor2-xkoor1)+sqr(ykoor2-ykoor1)).

Primov algoritam

Unošenjem ovih čvorova stanje u memoriji izgleda ovako,

Lista slobodnih čvorova Ls

Lista čvorova pridruženih stablu Lg

1	72	44
2	129	133
3	68	224
4	252	77
5	276	133
6	217	283

Prvi korak je prebacivanje prvog čvora iz Ls u Lg pa sada imamo,

Lista slobodnih čvorova Ls

Lista čvorova pridruženih stablu Lg

2	129	133
3	68	224
4	252	77
5	276	133
6	217	283

U narednom koraku mjerimo udaljenosti svih čvorova iz liste Lg sa svim čvorovima u listi Ls,čvor iz Ls najbliži stablu prebacijemo u Lg, korisnik vidi povučenu liniju između dva čvora i izvještaj u Memo komponenti koji glasi,

Grana 1-->4 u duzini 105,688220724923 mjernih jedinica.

Stanje memorije je sada,

Lista slobodnih čvorova Ls

Lista čvorova pridruženih stablu Lg

2	129	133
3	68	224
5	276	133
6	217	283

1	189	60
4	252	77

Iterativnim postupkom dobijamo sledeće izvještaje,

Grana 4-->3 u duzini 109,553639829994 mjernih jedinica.

Grana 4-->2 u duzini 135,14806694881 mjernih jedinica.

Grana 2-->5 u duzini 60,9261848469113 mjernih jedinica.

Grana 3-->6 u duzini 160,256045127789 mjernih jedinica.

UKUPNA DUZINA: 571,572157478427 MJERNIH JEDINICA.

Kraj Primovog algoritma...

a na koncu stanje memorije izgleda ovako,

Lista slobodnih čvorova Ls

Lista čvorova pridruženih stablu Lg

1	189	60
4	252	77
3	68	224
2	129	133
5	276	133
6	217	283

Korisnik na ekranu vidi slijedeću sliku,

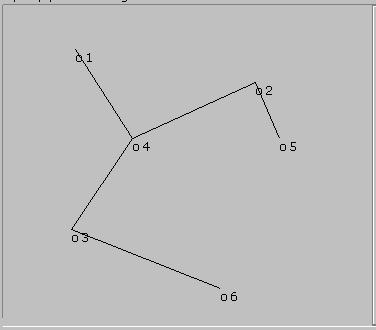
Slika 2. Pronađeno najkraće stablo grafa zadatog tačkama sa Slike1

Kruskalov algoritam

Koristimo isti brojni primjer.Uneseni čvorovi u listu Ls su,

Lista slobodnih čvorova Ls

1	72	44
2	129	133
3	68	224
4	252	77
5	276	133
6	217	283

Na osnovu ovih čvorova algoritam formira grane u vidu slogova sa sljedečim poljima,

imecvora1

xkoor1

ykoor1

imecvora2

xkoor2

ykoor2

duzina

fragment

sljedeci

Za nas su u ovom razmatranju bitna polja označena sivom bojom.Algoritam prvo formira sve kominacije (osim dupliranja) unesenih čvorova formirajući grane,

SPISAK SVIH MOGUCIH GRANA GRAFA:

Grana 2>5 u duzini 60,9261848469113 mjernih jedinica.

Grana 1>4 u duzini 105,688220724923 mjernih jedinica.

Grana 4>3 u duzini 109,553639829994 mjernih jedinica.

Grana 4>2 u duzini 135,14806694881 mjernih jedinica.

Grana 4>5 u duzini 147 mjernih jedinica.

Grana 3>6 u duzini 160,256045127789 mjernih jedinica.

Grana 5>6 u duzini 161,186227699515 mjernih jedinica.

Grana 4>6 u duzini 173,908021666627 mjernih jedinica.

Grana 1>3 u duzini 180,04443895883 mjernih jedinica.

Grana 1>2 u duzini 183 mjernih jedinica.

Grana 2>6 u duzini 208,95214763194 mjernih jedinica.

Grana 1>5 u duzini 222,569090396668 mjernih jedinica.

Grana 3>5 u duzini 227,035239555449 mjernih jedinica.

Grana 3>2 u duzini 235,510084709764 mjernih jedinica.

Grana 1>6 u duzini 279,546060605404 mjernih jedinica.

U grafičkoj prezentaciji lista Lk,izgleda ovako,

imecvora1	imecvora2	duzina	fragment
2	5	60,92618	0
1	4	105,6882	0
4	3	105,6882	0
4	2	135,1480	0
4	5	147,0000	0
3	6	160,2560	0
5	6	161,1862	0
4	6	173,9080	0
1	3	180,0444	0
1	2	183,0000	0
2	6	208,9521	0
1	5	222,5690	0
3	5	227,0352	0
3	2	235,5100	0
1	6	279,5460	0

Možemo primjetiti sortiranost liste grana,nepostojanje dupliranih grana i to da na početku postupka sve grane imaju vrijednost polja fragment jednaku 0.

Dodajmo prvu granu najkraćem stablu,tabela se mijenja tako da sada izgleda ovako,

imecvora1	imecvora2	duzina	fragment
2	5	60,92618	1
1	4	105,6882	0
4	3	105,6882	0

Šta se dogodilo?Algoritam uzima prvu granu 2à 5 i provjerava da li se čvorovi nalaze i u jednoj dotad obrađenoj grani.Očito tih grana nema pa se vrijednost fragmenta generički uvećava za 1 i grana se pridružuje najkraćem stablu .U narednom koraku obrađujemo granu 1à 4,isti slučaj kao maloprije pa je,

imecvora1	imecvora2	duzina	fragment
2	5	60,92618	1
1	4	105,6882	2
4	3	105,6882	0

Grana se pridružuje najkraćem stablu.U narednom koraku obrađuje se grana 4à 3 ,čvor 4 očito se već nalazi u dotad obrađenoj grani a čvor 3 ne i u ovom slučaju grana se priključuje najkraćem stablu a vrijednost polja fragment određena je najvećom vrijednosti ovog polja za svaki od čvorova u dotad obrađenim granama,pa je,

imecvora1	imecvora2	duzina	fragment
2	5	60,92618	1
1	4	105,6882	2
4	3	105,6882	2

Pogledajmo slijedeću granu u donjoj tabeli,

imecvora1	imecvora2	duzina	fragment
2	5	60,92618	1
1	4	105,6882	2
4	3	105,6882	2
4	2	135,1480	0
4	5	147,0000	0
3	6	160,2560	0

Grana 4à 2 ima najveću vrijednost fragmenta po čvoru 4 u dotada obrađenim granama jednaku 2 a po čvoru 2 ta vrijednost je 1.Čvorovi dakle pripadaju razlićitim fragmentima pa se i ova grana može uključiti u najkraće stabo,ali je sada potrebno sve grane koje pripadaju fragmentu 1 priključiti fragmentu 2(od dva dobijamo jedan fragmenat ),pa je,

imecvora1	imecvora2	duzina	fragment
2	5	60,92618	2
1	4	105,6882	2
4	3	105,6882	2
4	2	135,1480	2
4	5	147,0000	0
3	6	160,2560	0

Naredna grana 4à 5 ima po čvorovima iste vrijednosti fragmenta u dotad obrađenim granama,obadva čvora pripadaju istom fragment 2 i ako bismo izvršili priključenje ove grane zatvorili bi ciklus.Ovu granu zato preskačemo i ne priključujemo je najkraćem stablu.

Opisani proces iterativno ponavljamo sve dok ne obradimo sve grane grafa.

Obradili smo dakle sva 3 slučaja:

1. Ako se čvorovi grane koju unosimo ne pojavljuju u dotad obrađenim granama granu priključujemo najkraćem stablu,

2. ako se čvorovi pojavljuju ali u granama koje imaju različitu vrijednost polja fragment,granu priključujemo najkraćem stablu,i promijenimo vrijednost polja fragment tako da znamo da smo spajanjem dva fragmenta dobili novi jedinstveni fragment,

3. ako se čvorovi grane koju unosimo pojavljuju u dotad obrađenim granama ali po polju fragment te grane imaju istu vrijednost,tu granu preskaćemo i ne pridružujemo je najkraćem stablu grafa.

Na koncu , u konkretnom brojnom primjeru dobijamo izvještaj,

Dodata grana 2-5 u duzini 60,9261848469113.

Dodata grana 1-4 u duzini 105,688220724923.

Dodata grana 4-3 u duzini 109,553639829994.

Dodata grana 4-2 u duzini 135,14806694881.

Dodata grana 3-6 u duzini 160,256045127789.

UKUPNA DUZINA: 571,572157478427 MJERNIH JEDINICA.

Kraj Kruskalovog algoritma...

^*Napomena:Kako je slika rezultata ista kao Slika2 u brojnom primjeru za Primov algoritam ovdje je ne navodimo.

Zaključak

Problemi u toku izrade zadatka ,Prijedlozi

Najveći problem u izradi zadatka bio je sa implementacijom Kruskalovog algoritma jer on,za razliku od Primovog algoritma,sadrži zahtjevniju implementaciju provjere zatvaranja ciklusa.

S druge strane ovaj program se može uz dodatni trud dosta dobro razviti.Npr.u radnu površinu je moguće implementirati dodavanje predloška (template) npr. snimak nekog mjesta iz vazduha.Potrebno je dodati jednu edit kontrolu u koju bi korisnik unio razmjeru tog predloška npr.1:25000 pa je u mjerenju udaljenosti između dva čvora na trenutni oblik,

dmin = sqrt (sqr(xkoor2-xkoor1)+sqr(ykoor2-ykoor1));

potrebno dodati,

dmin = (sqrt (sqr(xkoor2-xkoor1)+sqr(ykoor2-ykoor1)))*razmjera*sirina_pixela;

pa bi rezultate dobijali u konkretnim mjernim jedinicama npr. u metrima.Naravno potrebno je napisati funkciju koja bi "pročitala" vrstu monitora korisnika radi utvrđivanja širine pixela ili ,olakšanja radi, prepustiti korisniku da to "upiše" u program uz upotrebu još jedne edit kontrole.

Korištena literatura^*

· "Operations research - Graph theory" Imperial College, J.E.Beasley

· Prim's Algorithm ,Kruskal's Algorithm Scott Gasch

· Prim's Algorithm ,Kruskal's Algorithm Kenji Ikeda

^*U pitanju su resursi pronađeni na Internetu